[코드트리 조별과제] 동적계획법

동적계획법

: 큰 문제에 대한 답을 얻기 위해 동일한 문제이지만 크기가 더 작은 문제들을 먼저 해결한 뒤, 그 결과들을 이용해 큰 문제를 비교적 간단하게 해결하는 기법

• for loop 이용
• 재귀함수 이용

메모이제이션

: 값을 기록하고, 그 기록한 값을 참조하는 것

• memoization 이용시에는 함수 도입부에 -1이 아닌 경우 memo 값을 반환해주는 코드를 작성
• 그렇지 않은 경우라면 반환해줘야 하는 값을 memo에 저장해준 뒤 해당 값을 반환해주면 됨
• 탑다운 방식

Tabulation

• for문 이용하는 방법
• Tabulation이용 시 배열의 이름은 보통 dp라고 지음
• 바텀업 방식

💡 이론적인 시간복잡도는 두 방법이 동일하나, 탑다운 방식은 함수를 재귀적으로 여러번 실행해야 하므로 함수 처리에 추가적인 시간이 약간 더 붙어 실제로는 바텀업 방식이 약간 더 빠르다..

 

subproblem을 그대로 합치면 되는 DP

타일채우기, BST 개수

*BST: 이진탐색트리

격자 안에서 한 칸씩 이동하는 경우

→ max 값 메모이제이션 해가면서 구하는거 …??

조건에 맞게 선택적으로 전진하는 경우

가장 긴 증가하는 부분 수열 (LIS; Longest Increasing Subsequence)

부분수열: 수열에서 일부 숫자를 선택해서 만든 또 다른 수열

• 첫 번째 숫자를 시작으로 계속 증가하는 값만 고른다고 해서 항상 LIS가 구해진다고 할 수 없음

dp[i] → 마지막으로 고른 원소의 위치가 i인 부분 수열 중 최장 증가 부분 수열의 길이

예) [10, 30, 25, 40, 28, 45]

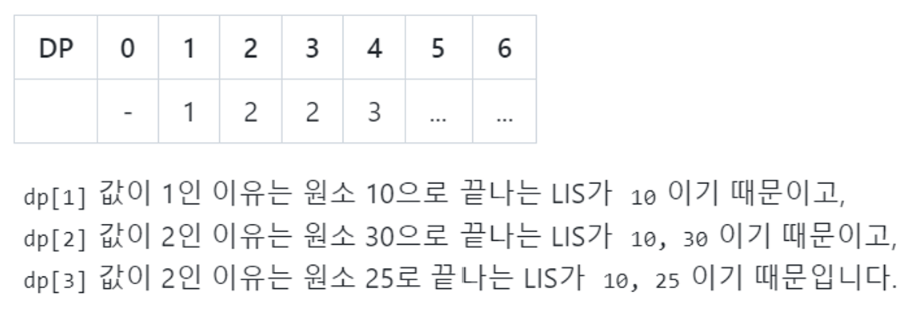
점화식

dp[i] = max(dp[j] + 1)

• 1 ≤ j < i

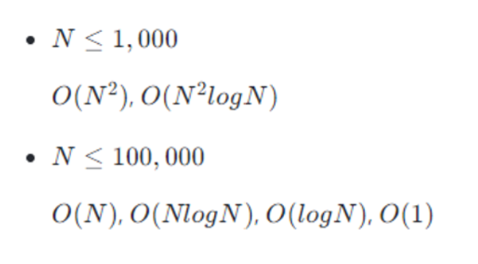
N≤ 1000 이면 dp 점화식 방식으로 for문으로 풀어도됨

이진탐색 방법으로 푸는 법

→ memo 1차원 배열에길이가 len인 부분증가수열들의 마지막 값 중 최솟값을 저장함

memo[len] = 0~i 의 arr 원소배열 중 LIS의 길이가 len인 부분수열들의 마지막 값 중 최솟값